Archive

Appearance

Return to top
On this page

Heap

우선순위 큐를 구현하기 위한 완전이진트리의 일종으로, 매 순회마다 최댓값 또는 최솟값을 얻고 싶을 때 유용한 구조입니다.

완전이진트리

이진트리의 높이가 h일 때, (h-1)까지는 모든 node들이 자식 node들을 2개씩 가지고 h에서부터 왼쪽부터 차례대로 채워진 형태를 가집니다.

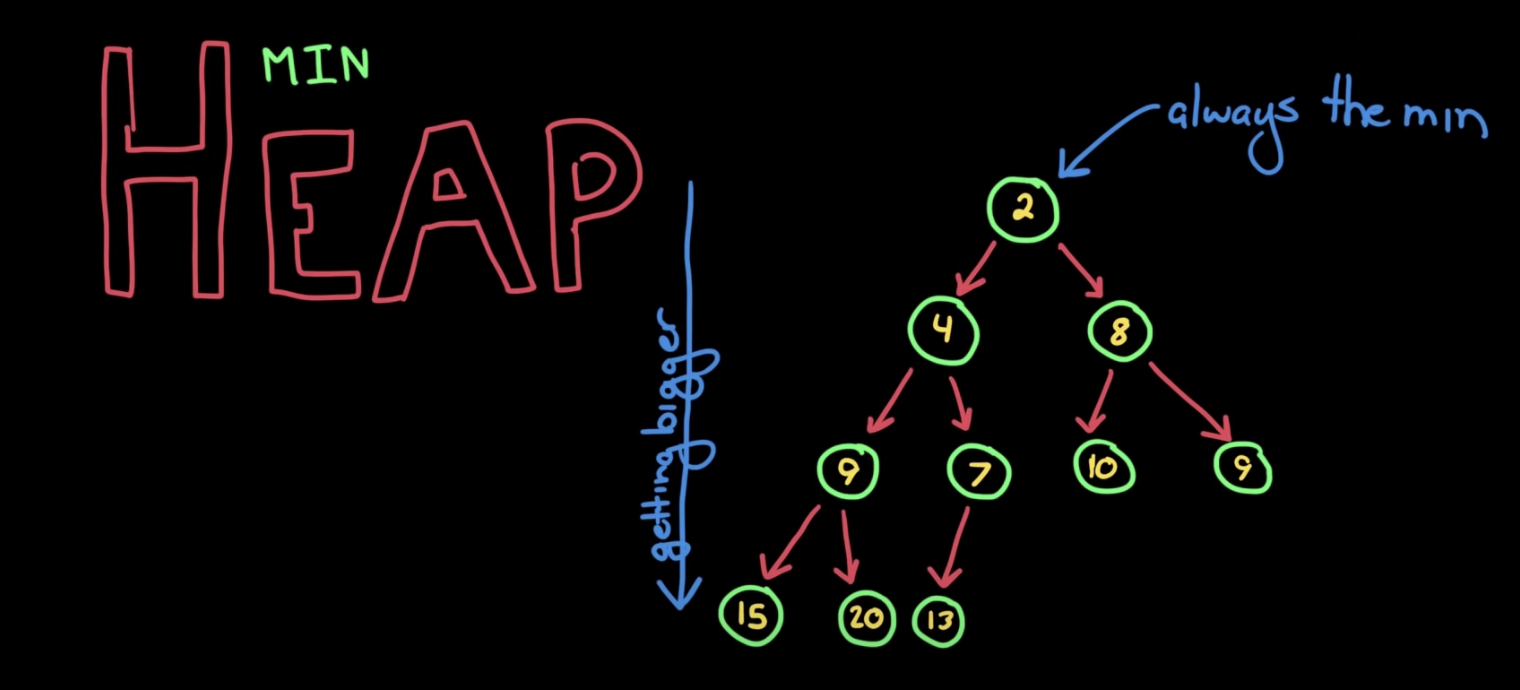
Min Heap

root node의 값이 하위 node들의 값보다 작습니다.

Min Heap

삽입

특정 node를 삽입할 때는 우선 가장 마지막에 append 합니다. 그 뒤에 자신보다 더 작은 값을 가진 부모 node를 찾을 때까지 depth를 올라갑니다.

root 제거

제일 마지막에 있는 node를 root로 지정하고 왼쪽, 오른쪽 자식 node들의 값보다 작을 때까지 depth를 내려갑니다.

Max Heap

Min Heap과 반대로 구현하면 됩니다!

구현코드

heap은 트리형태를 가지지만 root를 index 0으로 가지는 1차원 배열로 간결하게 나타낼 수 있습니다.

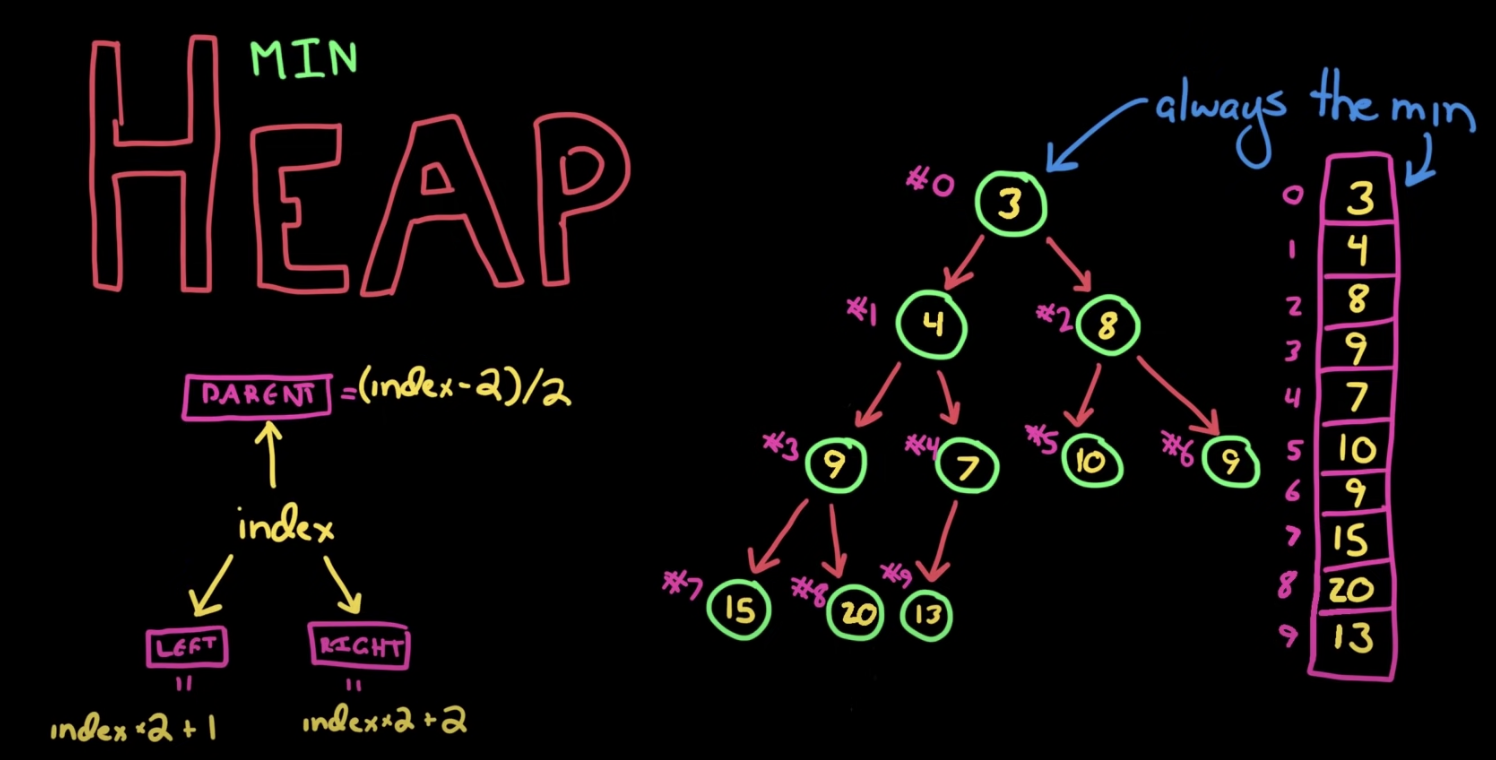
Heap Array

js
const heap = (cmpFn) => {
  let arr = [];

  const leftIdx = (idx) => 2 * idx + 1;
  const rightIdx = (idx) => 2 * idx + 2;
  const parentIdx = (idx) => Math.floor((idx - 1) / 2);

  const hasLeft = (idx) => leftIdx(idx) < heap.length;
  const hasRight = (idx) => rightIdx(idx) < heap.length;
  const hasParent = (idx) => 0 <= parentIdx(idx);

  const swap = (x, y) => {
    [arr[x], arr[y]] = [arr[y], arr[x]];
  };

  const add = (data) => {
    heap.push(data);
    for (let p = heap.length - 1; hasParent(p); ) {
      const pr = parentIdx(p);
      if (cmpFn(heap[pr], heap[p])) {
        break;
      }
      swap(p, pr);
      p = pr;
    }
  };

  // root 제거 + 반환
  const poll = () => {
    if (heap.length === 0) {
      return null;
    }
    if (heap.length === 1) {
      return heap[0];
    }

    const top = heap.shift();
    const last = heap.pop();

    if (heap.length) {
      heap.unshift(last);
      for (let p = 0; hasLeft(p); ) {
        let to = leftIdx(p);
        if (hasRight(p) && cmpFn(heap[rightIdx(p)], heap[to])) {
          to = rightIdx(p);
        }
        if (cmpFn(heap[p], heap[to])) break;
        swap(p, to);
        p = to;
      }
    }

    return top;
  };

  return {
    add,
    poll,
  };
};
js
const { ... } = heap((a, b) => a < b); // min-heap
const { ... } = heap((a, b) => a > b); // max-heap