Archive

Appearance

Return to top
On this page

DFS, BFS

DFS

시작 node부터 시작해서 자식 node마다 재귀적으로 경로를 검색하는 방식으로, 목적지 node에 도착할 때까지 반복합니다.

DFS

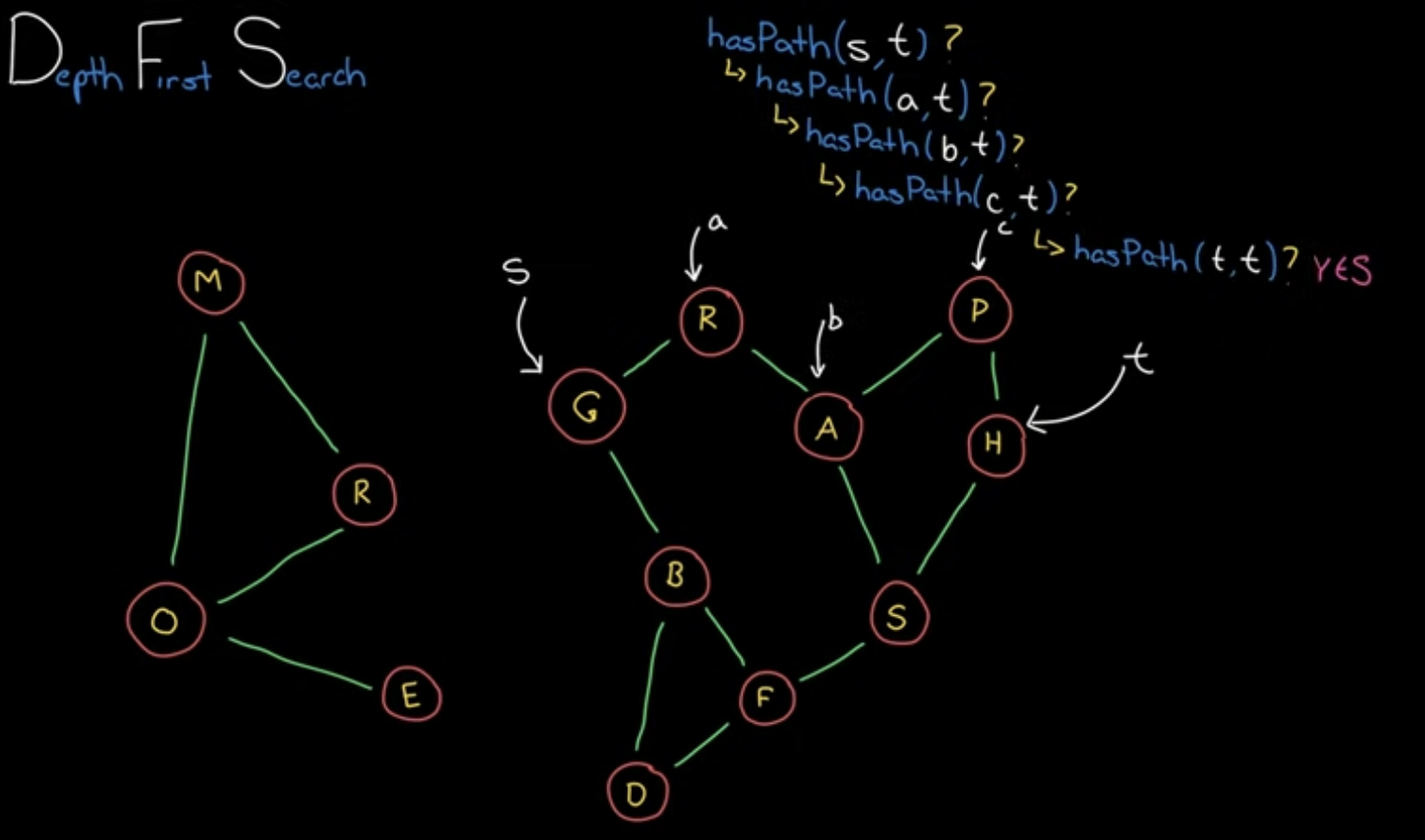
단거리로 갈 수 있음에도 불구하고 다른 경로를 택해서 우회하여 도착할 가능성이 다분하다는 단점이 있습니다.

보통 node X에서 node Y로의 경로 존재여부나 개수 등을 구할 때 자주 활용됩니다.

구현코드

js
//  정사각형 binary grid 형태로 제공된 그래프인 경우
const dfs = (adj) => {
  const visited = new Set();

  const hasPath = (src, dst) => {
    if (visited.has(src)) {
      return false;
    }
    if (src === dst) {
      return true;
    }

    visited.add(src);

    for (let next = src + 1; next < adj.length; next++) {
      // 다음 재귀를 시작하기 위한 조건은?
      if (adj[src][next] && hasPath(next, dst)) {
        return true;
      }
    }

    // 해당 케이스에 대한 탐색이 끝났으면 visited를 원래대로 돌려놓습니다.
    visited.delete(src);
  };

  return {
    hasPath,
  };
};

WARNING

안타깝게도 위 방식은 양방향 그래프에서만 활용할 수 있습니다.

단방향에서 임의의 두 노드 간의 경로 존재여부는 Floyd-Warshall Algorithm을 사용하면 됩니다.

BFS

시작 node부터 시작해서 자식 node가 목적지 node인지 여부를 level을 넓혀가면서 탐색하는 방식입니다.

BFS

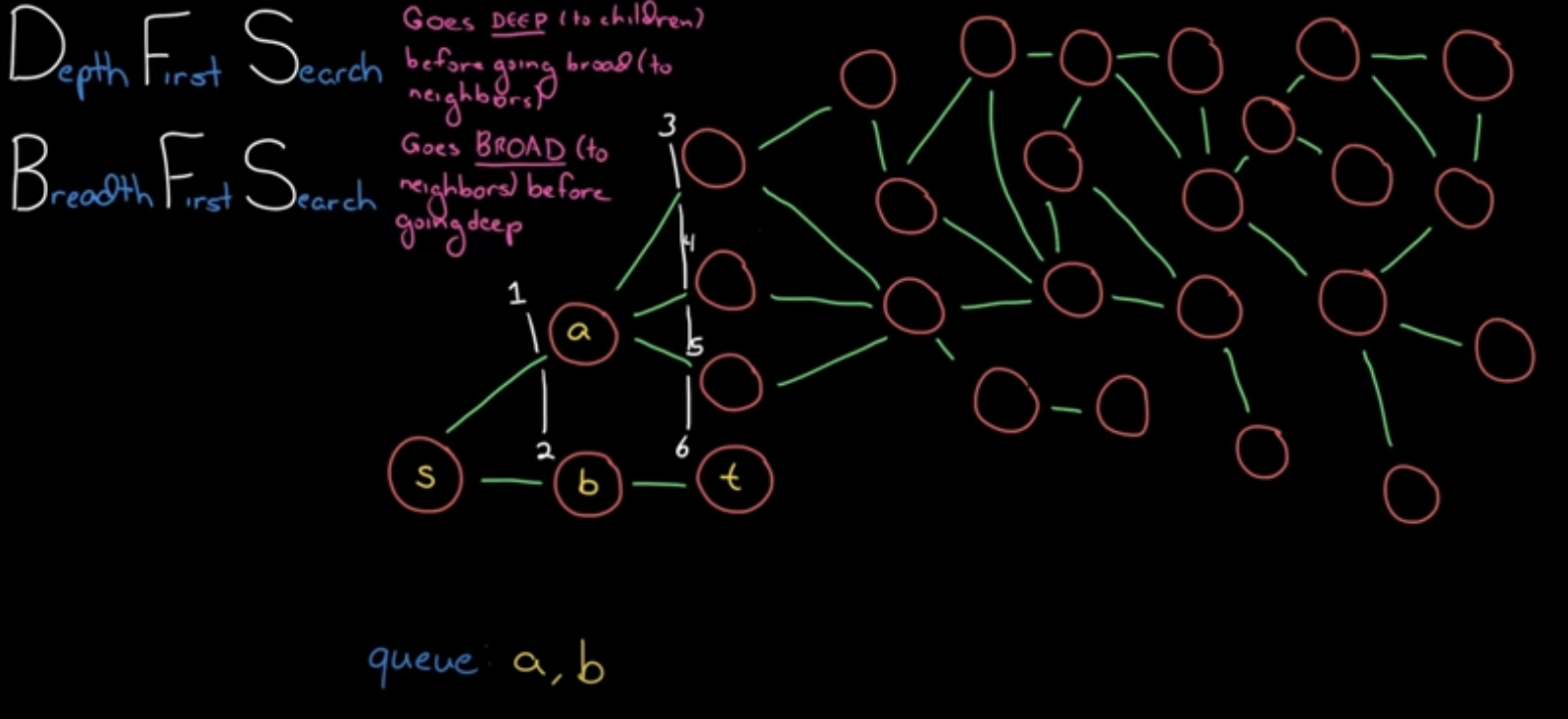
보통 queue로 구현하고, 특정 node로의 최단거리를 구할 때 자주 활용됩니다.

구현코드

js
const bfs = (adj) => {
  const q = [];
  const visited = new Set();

  const hasPath = (src, dst) => {
    q.push(src);

    while (q.length) {
      const x = q.shift();
      // 이미 방문한 node라면 다음 node를 뽑습니다.
      if (visited.has(x)) {
        continue;
      }
      if (x === dst) {
        return true;
      }

      visited.add(x);

      for (let c = x + 1; c < adj.length; c++) {
        // queue에 push하여 예약할 수 있는 조건은?
        adj[x][c] && q.push(c);
      }
    }

    return false;
  };

  return {
    hasPath,
  };
};

응용

  1. 미로에서 최소경로 구하기
js
const maps = [...] // 2차원 인접행렬로 주어진 미로
const [m, n] = [maps.length, maps[0].length];

const dx = [0, 1, 0, -1];
const dy = [1, 0, -1, 0];

const q = [[0, 0, 1]]; // q에 저장되는 지점 정보 : [x좌표, y좌표, 해당 지점까지 최단거리]
const visited = new Set();

while (q.length) {
  const [px, py, dist] = q.shift();
  const pStr = `${px}_${py}`;

  if (visited.has(pStr)) {
    continue;
  }

  if (px === m - 1 && py === n - 1) {
    return dist;
  }

  visited.add(pStr);

  for (let i = 0; i < 4; i++) {
    const [nx, ny] = [px + dx[i], py + dy[i]];

    if (nx < 0 || m <= nx || ny < 0 || n <= ny || !maps[nx][ny]) {
      continue;
    }
    q.push([nx, ny, dist + 1]);
  }
}

return -1;