Memoization, Dynamic Programming
재귀적으로 연산한 결과들을 캐시에 저장하고 필요할 때마다 조회하여 중복된 연산을 줄이는 작업을 memoization이라고 합니다.
큰 문제를 작은 문제로 분할해서 풀되 memoization을 이용하여 작은 문제의 답을 단순히 반환하는 방식으로 단 한번만 풀도록 하는 알고리즘이 바로 Dynamic Programming입니다.
Dynamic Programming의 조건
- 큰 문제를 1개 이상의 작은 문제들로 나눌 수 있습니다.
- 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일합니다.
TIP
문제에서 1234567과 같이 큰 수(NUM)로 나눈 나머지를 반환하는 것을 조건으로 제시하는 경우도 종종 있습니다.
이러한 경우에는 dp배열을 아래와 같이 나머지 값으로 업데이트하면 됩니다!
dp[i] = fn(dp[j] % NUM, dp[k] % NUM) % NUM;
피보나치 수열
피보나치의 수열을 기존 재귀적인 방법에 memoization을 적용하면 다음과 같이 구현할 수 있습니다.

const fibo = (n) => {
const dp = Array(n).fill(0);
const calc = (x = n) => {
if (x === 0) {
return 0;
} else if (x === 1) {
return 1;
}
if (!dp[x]) {
dp[x] = calc(x - 1) + calc(x - 2);
}
return dp[x];
};
return calc();
};
TIP
위 코드로 구현하면 공간복잡도는 시간복잡도와 동일하게 O(N) 입니다.
이는 cache를 구현하기 위한 배열과 memoize되지 않은 값을 구하기 위해 재귀호출을 진행하면서 누적된 콜스택의 크기가 모두 N이기 때문입니다!
길찾기
N x N 크기의 grid에서 두 지점 사이의 경로의 개수를 구하는 문제는 아래와 같이 재귀적으로 구할 수 있습니다.
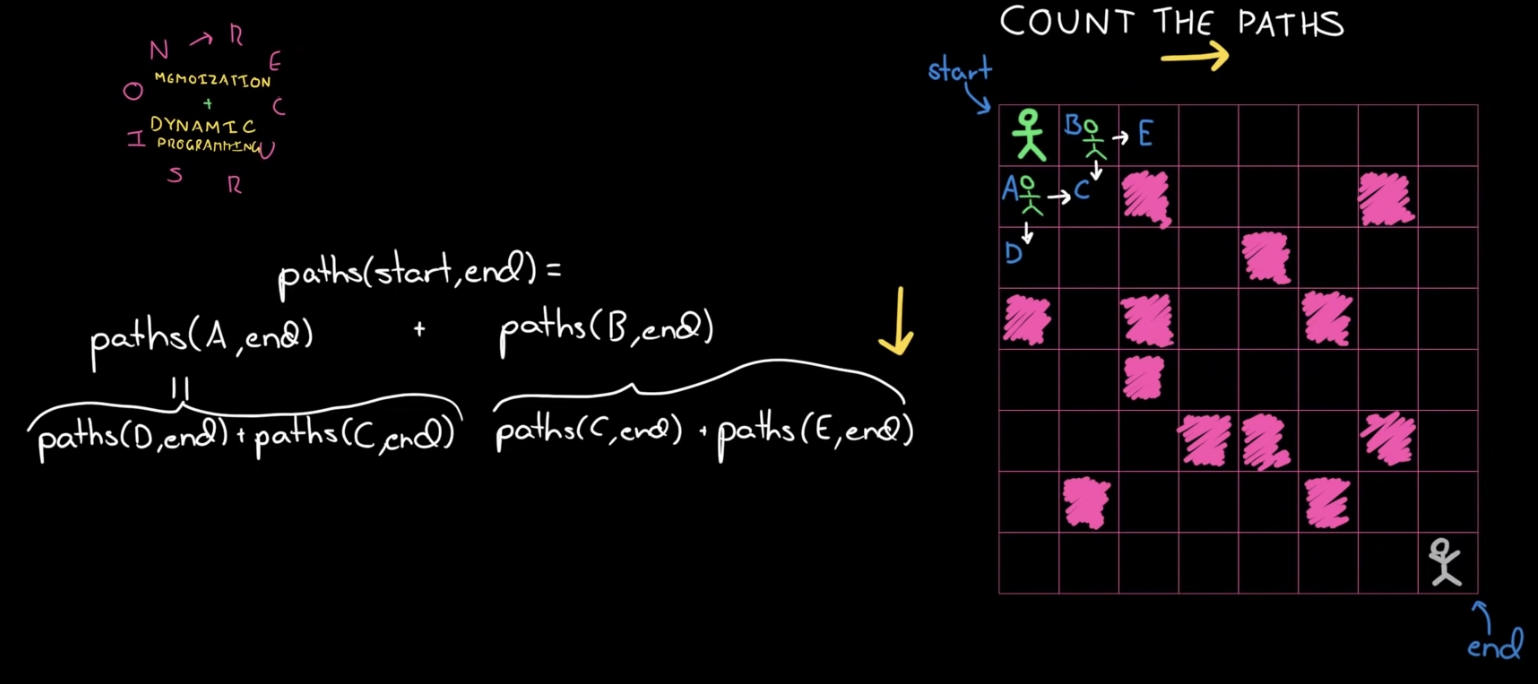
const countPaths = (grid) => {
const [endX, endY] = [grid.length - 1, grid[0].length - 1];
const calc = (x = 0, y = 0) => {
// 갈 수 없는 지점이 1로 표시한 grid인 경우
if (endX < x || endY < y || grid[x][y]) {
return 0;
}
if (x === endX && y === endY) {
return 1;
}
return calc(x + 1, y) + calc(x, y + 1);
};
return calc();
};
또는 특정 지점에서 도착지점까지 갈 수 있는 경로의 수를 memoize하는 방식으로도 구할 수 있습니다. 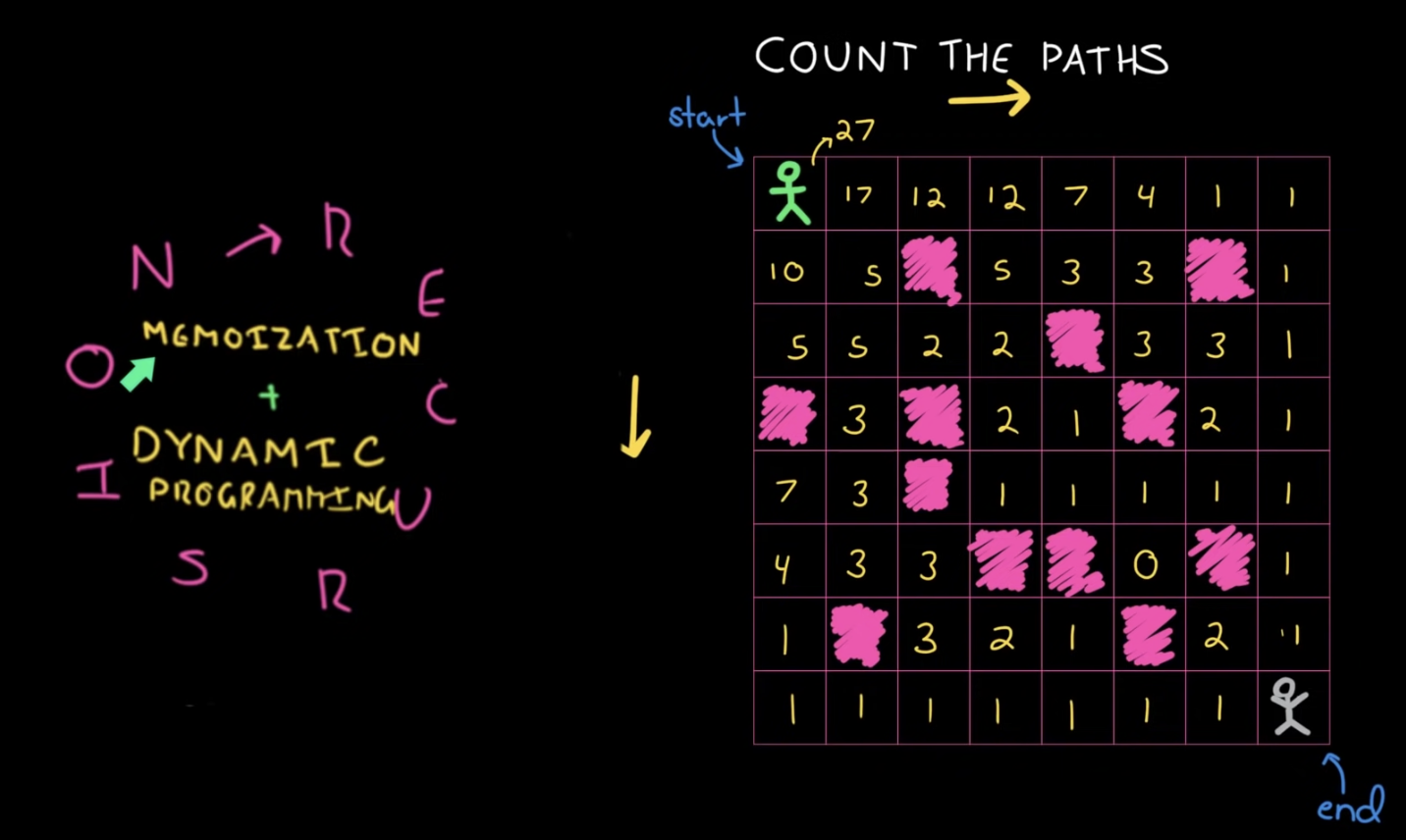
const countPaths = (grid) => {
const [rows, cols] = [grid.length, grid[0].length];
const dp = Array.from(Array(rows), () => Array(cols).fill(0));
for (let i = rows - 1; 0 <= i; i--) {
for (let j = cols - 1; 0 <= j; j--) {
if (i === rows - 1 && j === cols - 1) {
dp[i][j] = 1;
continue;
}
// 갈 수 없는 지점이 1로 표시한 grid인 경우
if (grid[i][j]) {
dp[i][j] = 0;
continue;
}
if (i === rows - 1) {
dp[i][j] = dp[i][j + 1];
continue;
}
if (j === cols - 1) {
dp[i][j] = dp[i + 1][j];
continue;
}
dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
}
}
return dp[0][0];
};
TIP
반대로 출발지점에서 특정지점까지 갈 수 있는 경로의 수를 memoize해도 결과는 동일하게 나옵니다!
// ...
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
if (i === 0 && j === 0) {
dp[i][j] = 1;
continue;
}
if (grid[i][j]) {
dp[i][j] = 0;
continue;
}
if (i === 0) {
dp[i][j] = dp[i][j - 1];
continue;
}
if (j === 0) {
dp[i][j] = dp[i - 1][j];
continue;
}
dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
}
}
return dp[rows - 1][cols - 1];
Floyd-Warshall Algorithm
인접행렬로 주어진 그래프에서 임의의 두 node간의 최단경로 또는 경로 존재여부를 모두 구하기 위한 알고리즘으로, 두 node 간의 거쳐가는 node에 따라 정보를 업데이트합니다.
여기서 단방향 그래프의 경우, 반대방향의 경로는 음수로 표현합니다.
// 두 노드간의 경로 존재여부
const edges = []; // [x, y][] : node x에서 node y 방향의 edge
const n = /* node의 개수 */;
const adj = Array.from(Array(n), () => Array(n).fill(null));
for (let i = 0; i < n; i++) {
adj[i][i] = 0;
}
for (const [x, y] of edges) {
adj[x][y] = 1;
adj[y][x] = -1;
}
for (let mid = 0; mid < n; mid++) {
// node i와 j 사이에서 경유하는 node mid
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
if (adj[i][mid] === 1 && adj[mid][j] === 1) {
adj[i][j] = 1;
continue;
}
if (adj[i][mid] === -1 && adj[mid][j] === -1) {
adj[i][j] = -1;
continue;
}
}
}
}
// 위 과정을 거친 뒤에도...
// adj[i][j]가 null이면 node i에서 node j로의 경로가 존재하지 않음을 의미합니다.
// adj[i][j]가 1 또는 -1이면 node i에서 j로 정방향 또는 역방향 경로가 존재함을 의미합니다.
3중 for문을 수행하므로 전체 시간복잡도는 O(N ^ 3)을 가집니다.