Sort
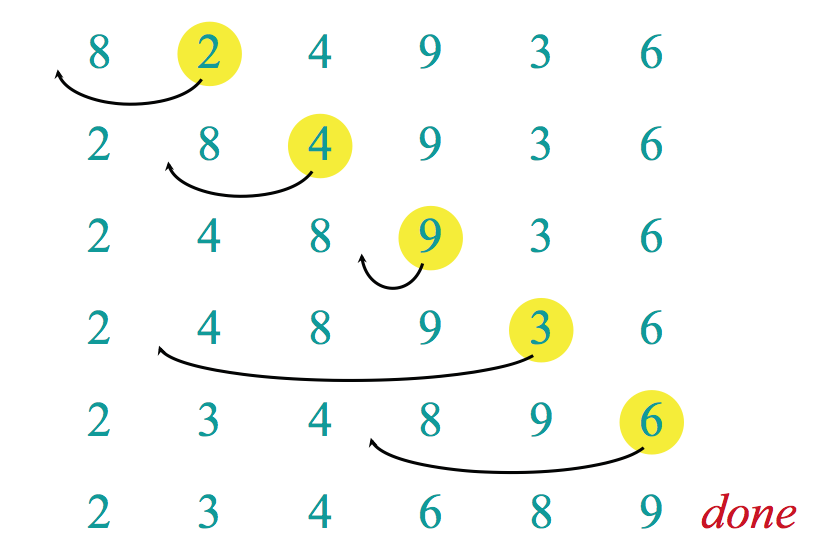
Insertion Sort
index 0에서부터 순회하면서 특정 요소를 앞에서 정렬된 배열에 적절한 위치에 삽입하는 방식으로, 최대 O(N^2)의 시간 복잡도를 가집니다.
js
const insertionSort = (compFn) => (arr) => {
const arr_c = [...arr];
for (let i = 0; i < arr_c.length; i++) {
const x = arr_c[i];
let j = i;
while (1 <= j) {
if (compFn(arr_c[j - 1], x)) {
break;
}
arr_c[j] = arr_c[j - 1];
j--;
}
arr_c[j] = x;
}
return arr_c.join(" ");
};
const 오름차순 = insertionSort((a, b) => a < b);
const 내림차순 = insertionSort((a, b) => b < a);
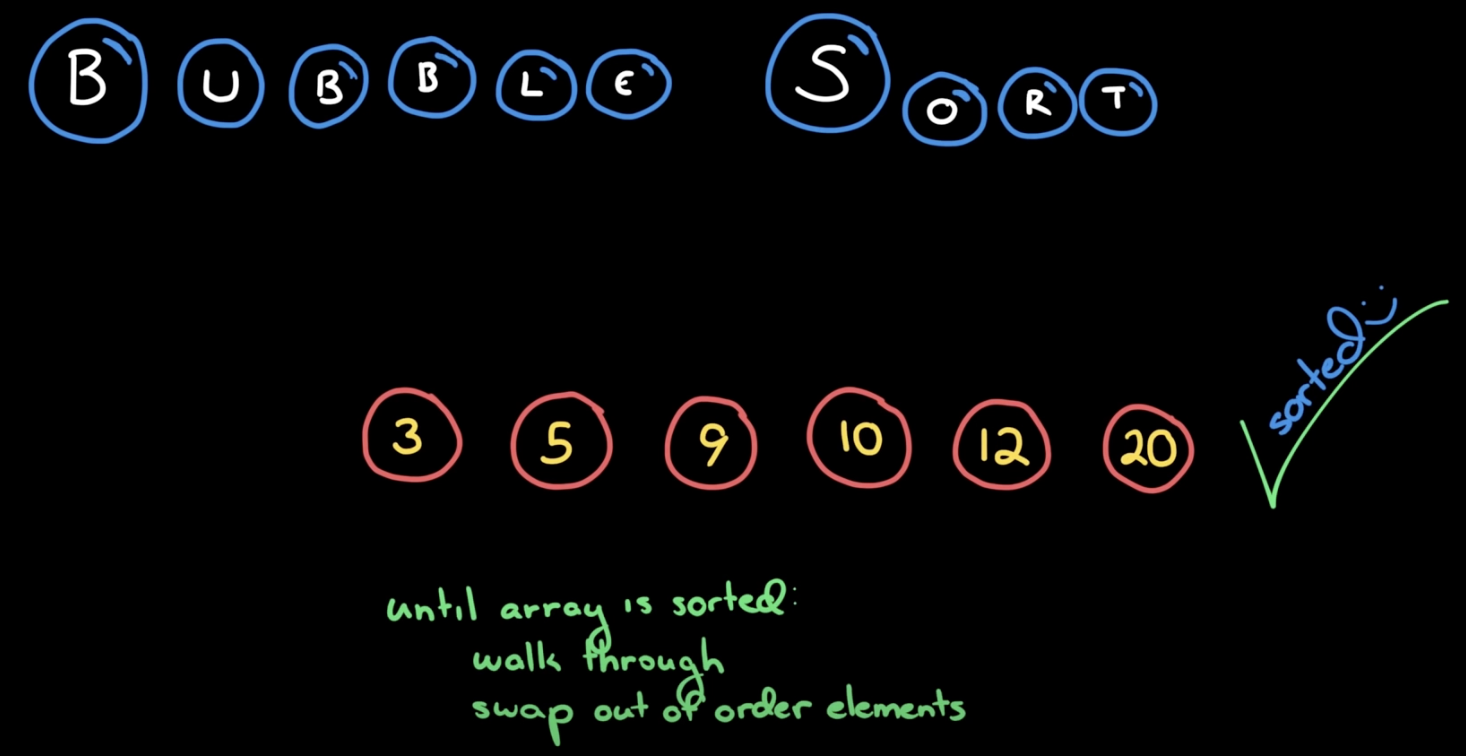
Bubble Sort
정렬이 될 때까지 수열을 순회할 때마다 바로 뒤의 있는 요소의 값이 더 작은 경우(오름차순 기준) swap하는 연산을 반복하는 방식입니다.
구현코드
js
const bubbleSort = (data) => {
const arr = [...data];
const swap = (x, y) => {
[arr[x], arr[y]] = [arr[y], arr[x]];
};
let lastIndex = arr.length - 1;
let isSorted = false;
while (!isSorted) {
isSorted = true;
for (let i = 0; i < lastIndex; i++) {
if (arr[i] < arr[i + 1]) continue;
swap(i, i + 1);
isSorted = false;
}
// 순회가 끝날 때마다 최댓값이 가장 마지막 index부터 차례대로 위치하므로
// 순회하는 범위를 하나씩 줄일 수 있습니다.
lastIndex--;
}
return arr;
};
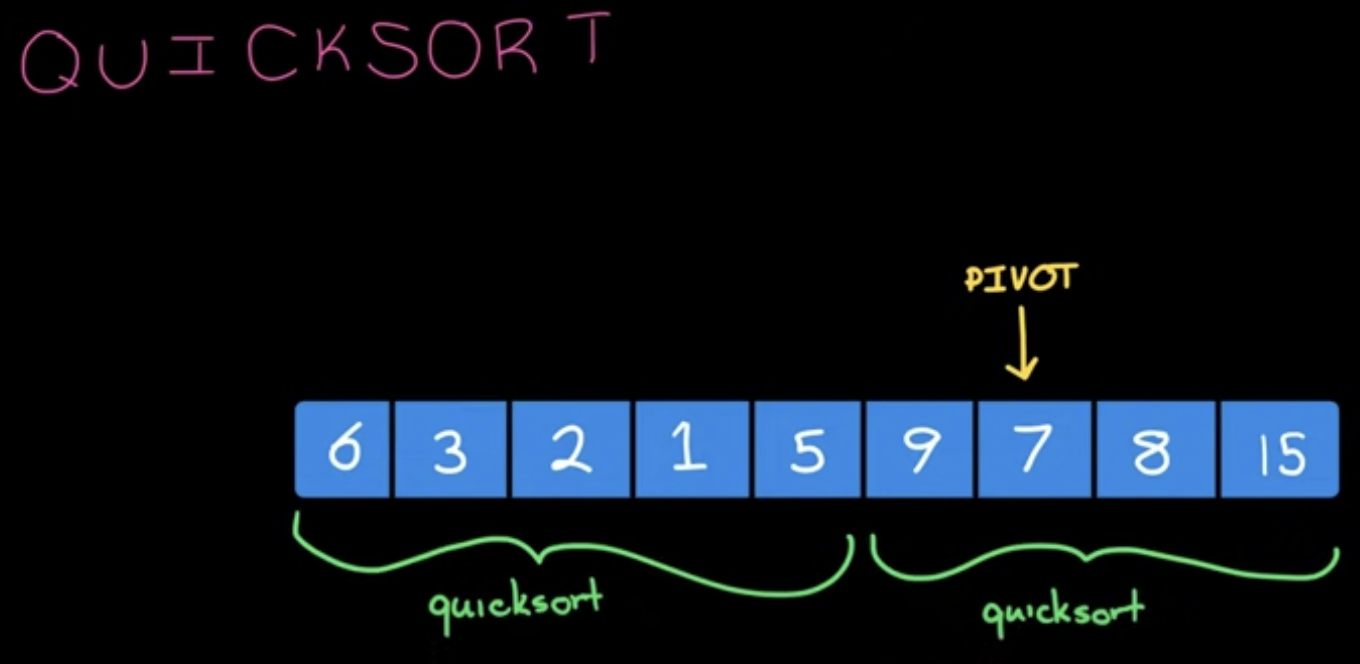
Quick Sort
분할정복 방식을 이용한 정렬입니다.
대상 수열에서 임의의 pivot(중심요소)를 선택하고 pivot 앞으로 pivot보다 작은 수, 뒤로 pivot보다 큰 수가 오도록 swap연산으로 수열을 두 영역으로 나누는데, 이러한 과정을 재귀적으로 수행합니다.
구현코드
js
const quickSort = (data) => {
const arr = [...data];
const swap = (x, y) => {
[arr[x], arr[y]] = [arr[y], arr[x]];
};
const partition = (x, y, pivot) => {
while (x <= y) {
while (arr[x] < pivot) {
x++;
}
while (pivot < arr[y]) {
y--;
}
if (x <= y) {
swap(x, y);
x++;
y--;
}
}
return x;
};
const sort = (left = 0, right = arr.length - 1) => {
// left와 right가 같다면 배열의 길이가 1이므로 정렬할 필요없습니다.
if (right <= left) return;
const pivot = arr[Math.floor((left + right) / 2)];
const index = partition(left, right, pivot);
sort(left, index - 1);
sort(index, right);
};
sort();
return arr;
};
대상 수열의 크기를 거의 반으로 분할할 때마다 총 N개의 요소들이 비교연산을 거치므로 시간복잡도는 O(NlogN)이지만 pivot을 첫번째 요소 또는 마지막 요소로 계속 유지하는 경우 O(N^2)의 복잡도가 나올 수도 있습니다.
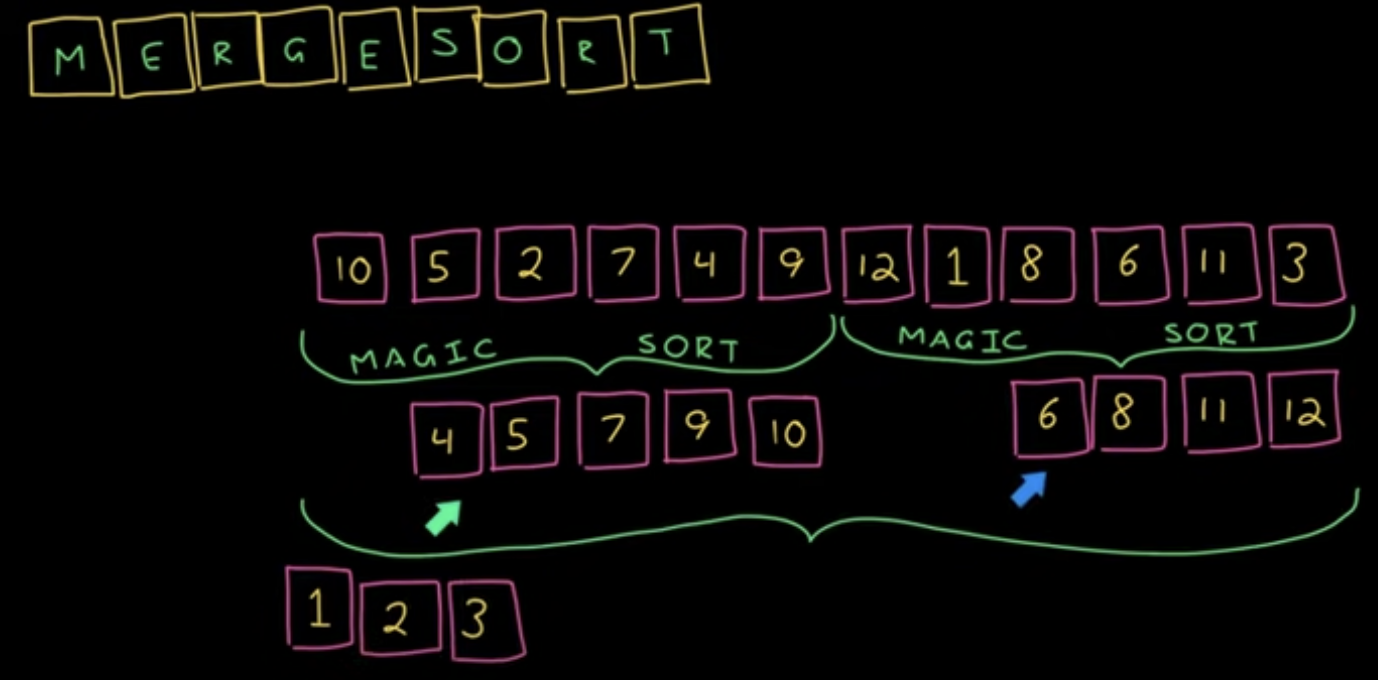
Merge Sort
quick sort처럼 분할정복을 이용합니다.
크기를 반으로 나눈 부분수열들을 각각 정렬한 뒤, 두 수열의 개별요소들을 오름차순(또는 내림차순)으로 결합하여 완성합니다.
구현코드
js
const mergeSort = (data) => {
// 모든 재귀함수에서 공통으로 사용할 연습장 배열
const temp = [...data];
// 실제 정렬된 배열
const arr = [...data];
const sort = (start = 0, end = data.length - 1) => {
if (end <= start) return;
const middle = Math.floor((start + end) / 2);
// 반으로 나눠서 각자 정렬 진행 + arr에 반영합니다.
sort(start, middle);
sort(middle + 1, end);
let [x, y, t] = [start, middle + 1, start];
while (x <= middle && y <= end) {
if (arr[x] <= arr[y]) {
temp[t++] = arr[x++];
} else {
temp[t++] = arr[y++];
}
}
// 아직 temp에 추가하지 못한 부분수열을 순회하여 마저 추가합니다.
for (let i = x; i <= middle; i++) {
temp[t++] = arr[i];
}
for (let i = y; i <= end; i++) {
temp[t++] = arr[i];
}
// temp에 정렬된 상태를 그대로 arr에 반영합니다.
for (let i = start; i <= end; i++) {
arr[i] = temp[i];
}
};
sort();
return arr;
};
Array.prototype.sort
V8 엔진 상에서 Merge Sort와 Insertion Sort를 결합한 Tim Sort 알고리즘을 사용하는데 최대 O(N*logN)의 시간 복잡도를 가집니다.
Counting Sort
배열의 요소들끼리 비교하는 것이 아닌 요소들의 빈도수를 사용하여 정렬된 배열을 생성하는 방식입니다.
여기서 요소는 number형이고 빈도수 배열의 index는 모든 요소들의 값을 포함해야 합니다.
js
const countingSort = (arr) => {
const freq = Array(Math.max(...arr) + 1).fill(0);
const ans = [];
for (const n of arr) {
freq[n]++;
}
for (let i = 0; i < freq.length; i++) {
ans.push(...Array(freq[i]).fill(i));
}
return ans;
};