Functor, Category
Functor
타입 A에서 타입 B으로 매핑하는 메서드를 가진 interface로, 매핑한 결과도 functor가 나옵니다.
JS에서 흔히 볼 수 있는 functor(mappable)로 Array, Promise, Stream 등이 있습니다.
functor의 사용이점들은 다음과 같습니다.
- 내부 데이터의 구체적인 값을 알지 않아도 타입만 안다면 매핑을 구현할 수 있다.
- functor 안에 데이터가 없어도 매핑로직은 그대로 수행된다.
- functor 내부 데이터에 적용할 매핑 함수들을 하나의 합성함수로 구현할 수 있다.
Category
functor는 원래 추상 대수학의 이론인 Category Theory에서 사용하는 용어입니다.
특정 category에서 다른 category로의 구조를 보존하는(= functor를 매핑한 결과는 functor가 나오는) 매핑을 구현하는 개체를 가리킵니다.
Category Theory에서 functor 내부의 데이터를 object, 매핑 콜백함수를 arrow(morphism)라고 칭합니다.
TIP
처음 소개하는 부분에서 "타입"은 바로 object의 데이터 타입을 의미합니다!
Functor Laws
Identity
functor 내부 데이터를 받아서 그대로 반환하는 매핑을 구현할 수 있습니다.
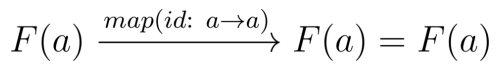
jsx
const a = [20];
const b = a.map((a) => a);
console.log(a.toString() === b.toString());
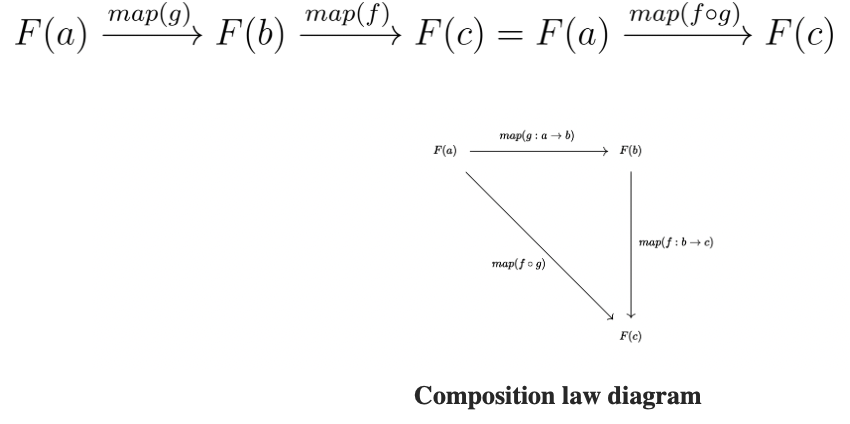
Composition
functor 내부 데이터에 대해서 연속으로 여러 번 매핑한 결과는 하나의 합성함수로 매핑한 결과와 동일합니다.
역으로 단일 arrow에 의한 매핑을 다수 arrow들의 연속된 매핑으로도 구현할 수 있습니다.
JS로 functor를 구현하면 다음과 같다.
js
const Functor = (value) => ({
map: (fn) => Functor(fn(value)),
});
const trace = (x) => {
console.log(x);
return x;
};
js
const u = Functor(2);
// Identity
const r1 = u; // Functor(2)
const r2 = u.map((x) => x); // Functor(2)
r1.map(trace); // 2
r2.map(trace); // 2
// Composition
const f = (n) => n + 1;
const g = (n) => n * 2;
const r3 = u.map((x) => f(g(x))); // Functor(5)
const r4 = u.map(g).map(f); // Functor(5)
r3.map(trace); // 5
r4.map(trace); // 5
커리함수를 사용하면 arrow를 고정하여 동일한 타입의 여러 functor들에 적용할 수 있습니다.
js
// curry 함수 활용
const mmap = (fn) => (mappable) => mappable.map(fn);
const log = (x) => console.log(x);
const double = (n) => n * 2;
const mdouble = mmap(double);
mdouble(Functor(4)).map(log); // 8
mdouble([4]).map(log); // 8